728x90
문제
https://www.acmicpc.net/problem/1937
n × n의 크기의 대나무 숲이 있다. 욕심쟁이 판다는 어떤 지역에서 대나무를 먹기 시작한다. 그리고 그 곳의 대나무를 다 먹어 치우면 상, 하, 좌, 우 중 한 곳으로 이동을 한다. 그리고 또 그곳에서 대나무를 먹는다. 그런데 단 조건이 있다. 이 판다는 매우 욕심이 많아서 대나무를 먹고 자리를 옮기면 그 옮긴 지역에 그 전 지역보다 대나무가 많이 있어야 한다.
이 판다의 사육사는 이런 판다를 대나무 숲에 풀어 놓아야 하는데, 어떤 지점에 처음에 풀어 놓아야 하고, 어떤 곳으로 이동을 시켜야 판다가 최대한 많은 칸을 방문할 수 있는지 고민에 빠져 있다. 우리의 임무는 이 사육사를 도와주는 것이다. n × n 크기의 대나무 숲이 주어져 있을 때, 이 판다가 최대한 많은 칸을 이동하려면 어떤 경로를 통하여 움직여야 하는지 구하여라.
[ 입력 ]
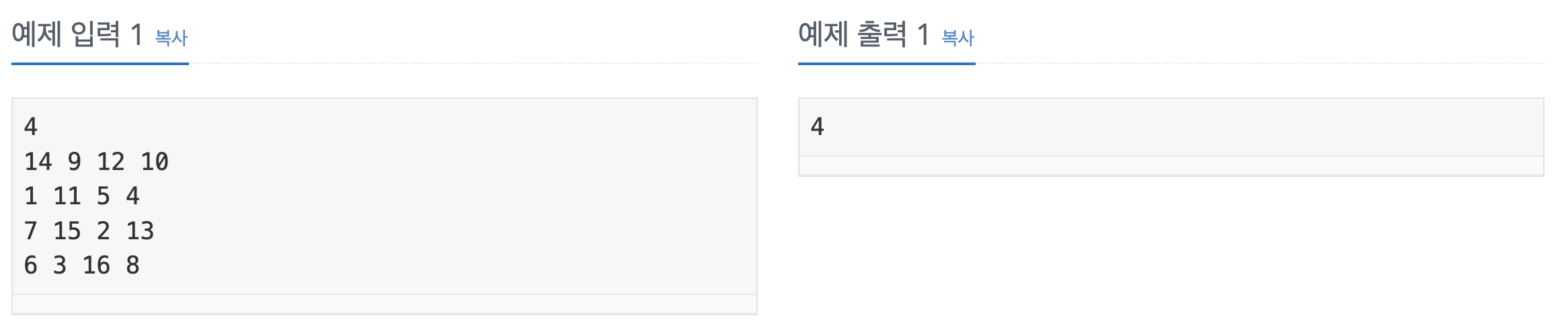
첫째 줄에 대나무 숲의 크기 n(1 ≤ n ≤ 500)이 주어진다. 그리고 둘째 줄부터 n+1번째 줄까지 대나무 숲의 정보가 주어진다. 대나무 숲의 정보는 공백을 사이로 두고 각 지역의 대나무의 양이 정수 값으로 주어진다. 대나무의 양은 1,000,000보다 작거나 같은 자연수이다.
[ 출력 ]
첫째 줄에는 판다가 이동할 수 있는 칸의 수의 최댓값을 출력한다.
풀이
- dfs와 dp를 이용해서 푸는 문제
// 백준 - 욕심쟁이 판다(1937)
import java.io.BufferedReader
import java.io.InputStreamReader
import java.util.StringTokenizer
import kotlin.math.max
val dx = arrayOf(1, -1, 0, 0)
val dy = arrayOf(0, 0, 1, -1)
var N = 0
var bamboo: Array<Array<Int>> = Array(1, {Array(1, {0})})
var dp: Array<Array<Int>> = Array(1, {Array(1, {0})})
var maxMove = 0
fun main() {
val br = BufferedReader(InputStreamReader(System.`in`))
N = br.readLine().toInt()
bamboo = Array(N, {Array(N, {0})})
dp = Array(N, {Array(N, {0})})
for(i: Int in 0..N-1) {
val st = StringTokenizer(br.readLine())
for(j: Int in 0..N-1) {
bamboo[i][j] = st.nextToken().toInt()
}
}
// 모든 칸마다 출발지점으로 했을 때 최대 이동칸수 구하고 그 중 최대값 찾기
for(i: Int in 0..N-1) {
for(j: Int in 0..N-1) {
maxMove = max(dfs(i, j), maxMove)
}
}
print(maxMove)
}
// 판다 이동
fun dfs(x: Int, y: Int) : Int {
// 이미 방문했던 값이 있다면
if(dp[x][y] != 0) return dp[x][y]
// 현재 칸은 무조건 먹기 때문에 1
dp[x][y] = 1
// 상하좌우 이동
for(i: Int in 0..3) {
val moveX = x + dx[i]
val moveY = y + dy[i]
// 공간을 벗어나면 패스
if(moveX < 0 || moveX >= N || moveY < 0 || moveY >= N) continue
// 현재 위치보다 대나무가 더 많은 경우 이동
if(bamboo[x][y] < bamboo[moveX][moveY]) {
// 해당 방향으로 이동한 것과 아닌 것 중 판다가 더 많이 이동하는 경우를 저장
dp[x][y] = max(dp[x][y], dfs(moveX, moveY) + 1)
}
}
return dp[x][y]
}
728x90
'Programming > Kotlin' 카테고리의 다른 글
| [백준/Kotlin] 불(5427) (0) | 2024.05.07 |
|---|---|
| [백준/Kotlin] 알약(4811) (0) | 2024.05.06 |
| [백준/Kotlin] 계란으로 계란치기(16987) (0) | 2024.05.05 |
| [백준/Kotlin] 소문난 칠공주(1941) (0) | 2024.05.05 |
| [Kotlin] 입력값 받기 (BufferedReader, InputStreamReader, StringTokenizer) (0) | 2024.05.04 |